Predicting the future

Most people would say that predicting the future is very hard to do, and in many ways they are right. In many situations, predicting the future is an extremely difficult task. For example, accurately predicting who will win the UEFA Champions League in 5 years time is not easy.  Even more difficult is predicting the lottery. The odds of correctly predicting the UK National Lottery numbers are estimated to be about 1 in 45 million. From which, one might be tempted to say, predicting the future cannot be done with any accuracy. However this is not the case, because there are many instances when we can predict the future with great accuracy.   

Engineering and prediction

Although most people don’t realise it, engineers are in the business of predicting the future. Engineers design machines and structures (e.g., cars, bridges, telephones, computers, etc.) that they predict will work. Then they build them, and they work as predicted, and we all use them every day. Consider for example, the amazing fact that 2.9 million passengers fly in and out of U.S. airports every day on 45,000 flights. When each one of these flights takes off, the passengers and crew onboard, as well as the Federal Aviation Administration, predict that their plane will land safely at the specified destination (otherwise no one would fly), and barring very occasional accidents (five fatal accidents among 32.2 million flights in 2022), their predictions come true with almost 100% accuracy.

So, what is the difference between say choosing the winning lottery ticket and predicting whether or not a passenger aircraft will fly safely across the Atlantic Ocean? Well, one is a completely random process with a high degree of uncertainty, and the other is a highly deterministic process that is very well understood. In short, the less well we understand about a system, the more uncertainty there is, and the harder it is to predict how it will behave.

Not random but complex

While some systems are truly random (e.g., roulette wheels, dice, the lottery, etc.), most are not. What they are, is complex, with underlying rules that are deterministic that are overlaid by random factors which cause variations in the observed output. Often, such systems are very complex and poorly understood, causing some to mistakenly believe that things are happening by chance. But this is not the case, because if we can understand the deterministic relationships underpinning the observed behaviour, then we can make an attempt at predicting how the system might behave in the future. Of course, the accuracy of any predictions made will depend on how well we understand the behaviour of the underlying system and the magnitude of the random perturbations that affect it.    

With truly random systems like the lottery, we can’t make predictions. All we can do is guess! However, because most systems encountered in real life are not random, but rather, based on deterministic rules (governed by physics, economics, the law, etc.) that are affected by chance events, it means that making predictions is possible. However, the accuracy of any predictions made will depend on how much information we have, and how much we understand the behaviour of the system. Remember, the greater the uncertainty, the more our predictions will look like guesswork.

Central tendency and probability

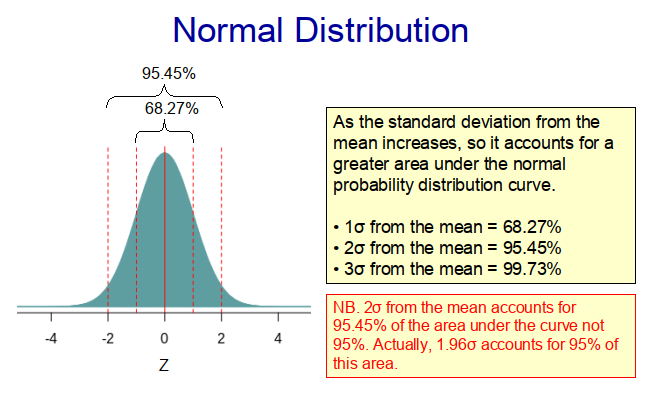
Having said this, even when we don’t fully understand the drivers of a particular system, we can still make predictions, if we know the distibution of the output variable. This is because central tendency dictates that in most instances the output variable will be relatively close to the median value of the distribution. For example, with a normal distribution, 68.27% of the observations lie within one standard deviation of the median (which is also the mean) value. This means that if we randomly select a value from the population, it is much more likely to come from the middle of the distribution than from its extremities. In other words, there is a tendency for observations to come from the centre of the distribution rather than from its extremities.

Armed with this information and a knowledge of statistical methods we can use the characteristics of the distribution of output variable to calculate the probability that an event of a certain magnitude is likely to occur. This is how bookmakers predict soccer match odds, because they know that the number of goals scored by the oposing teams will approximately conform to a Poisson distribution.

Copyright: Clive Beggs