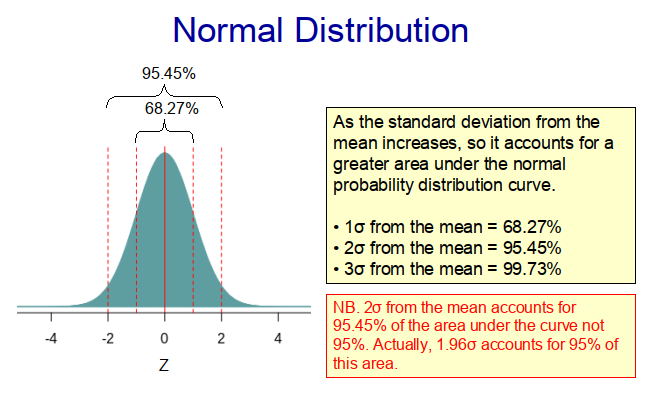
When we take samples from populations in nature, we often find that the distribution of the sample conforms approximately to a normal (Guassian) distribution, such as that shown in Figure 1 below. This is because the populations themselves exhibit a normal distribution. With this type of distribution, most of the observations lie somewhere near the middle of the range, with much fewer lying at the extremities. Indeed, with a true normal distribution, 68.27% of the observations lie within one standard deviation of the mean. This means that if we randomly select a value from the population, it is much more likely to come from the middle of the distribution than from its extremities. In other words, there is a tendency for observations to come from the centre of the distribution rather than from its extremities. Therefore, a value near the centre of the distribution is likely to be fairly representative of many of the ‘subjects’ within a given population.
In statistics a measure of ‘central tendency’ is a value that is typical or central for any given probability distribution. As such, it is a single value that attempts to describe a data set by identifying the central position within the data. The arithmetic mean (or average) is the most commonly used measure of central tendency, although the median and mode are also often used. These three measures of central tendency can be summarized as follows:
- The arithmetic mean (average) is the sum of all the measurements divided by the number of observations in the sample or data set.
- The median is the middle value that splits the data in half, with 50% above this value and 50% lower than it.
- The mode is the most frequent value that occurs in the data set.
When data is normally distributed, as is often the case in biology, medicine and social science, the mean, median and mode values will be equal, or approximately equal, to each other. Whereas, when the data has a skewed distribution the mean, median and mode values will not be equal.
When considering ordinal data, where the intervals between the data points are inconsistent or irregular, it is important to remember that the median and the mode are the only true measures of central tendency that can be used. Having said this, with such data, if the intervals are approximately equal (as with some Likert scales), then the mean may also be of some value as an approximate measure of central tendency. With nominal categorical data, because it has no intrinsic order, the mode is the only central tendency measure that can be used.
Copyright: Clive Beggs